EQUATIONS CONTAINING VARIABLES UNDER ONE OR MORE RADICALS

Recall the following:

• In order to solve for the unknown variable, you must isolate the variable.
• In the order of operations, multiplication and division are completed before addition and subtraction.
• In order to solve for x, you must isolate x.
• In order to isolate x, you must remove it from under the radical.
• If there are three radicals in the equation,isolate one of the radicals.
• Then raise both sides of the equation to a power equal to the index of the isolated radical.
• Isolate the remaining radical.
• Raise both sides of the equation to a power equal to the index of the isolated radical.
• You should now have a polynomial equation. Solve it.
• Remember that you did not start out with a polynomial; therefore, there may be extraneous solutions. Therefore, you must check your answers.

Solve for x in the following equation.

Problem 2.5d:

Answer: x=10.

Solution

First make a note of the fact that you cannot take the square root of a negative number. Therefore,the term is valid only if 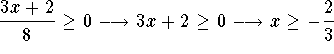, the term 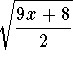is valid if , and the term is valid only if 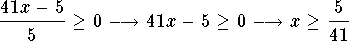. The equation is valid if all three terms are valid, therefore the domain is restricted to the common domain of the three terms or the set of real numbers

Square both sides of the equation and simplify.

Isolate the term and simplify.

Square both sides of the equation and simplify.

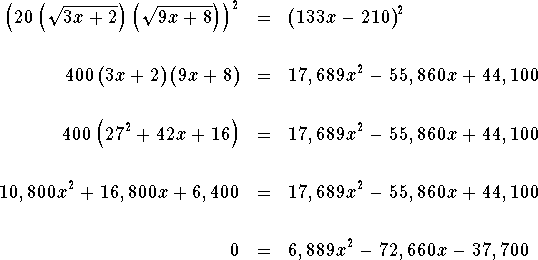
Use the quadratic formula to solve for x.

The answers are x=10 and 0.547249 (rounded).

Check the solution by substituting 10 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

• Left side: .
• Right Side:

Since the left side of the original equation equals the right side of the original equation after we substituted 10 for x, then x=10 is a solution.

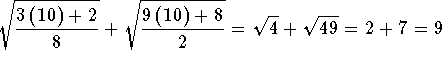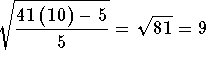
Check the solution by substituting 0.547249 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

• Left side:
• Right Side:

Since the left side of the original equation does not equal the right side of the original equation after we substituted 0.547249 for x, then the solution x=0.547249 is a not valid and not a solution after all.

You can also check the answer by graphing the equation:

The graph represents the right side of the original equation minus the left side of the original equation. The x-intercept(s) of this graph is(are) the solution(s). Since there is just one x-intercept at 10, then the only solution is x=10.

If you would like to go back to the problem page, click on problem.

If you would like to go back to the equation table of contents, click on Contents.

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA