 EQUATIONS CONTAINING VARIABLES UNDER ONE OR MORE RADICALS
EQUATIONS CONTAINING VARIABLES UNDER ONE OR MORE RADICALS

Recall the following:
- In order to solve for x, you must isolate x.
- In order to isolate x, you must remove it from under the
radical.
- If there are two radicals in the equation, isolate one of the
radicals.
- Then raise both sides of the equation to a power equal to the
index of the isolated radical.
- Isolate the remaining radical
- Raise both sides of the equation to a power equal to the index
of the isolated radical.
- You should now have a polynomial equation. Solve it.
- Remember that you did not start out with a polynomial;
therefore, there may be extraneous solutions. Therefore, you must
check your answers.
Work the following problems. Click on solution, if you want to review
the solutions.
Problem 2.5a:
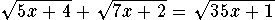
Solution.
Problem 2.5b:
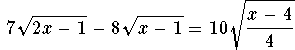
Solution.
Problem 2.5c:
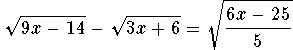
Solution.
Problem 2.5d:
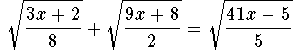
Solution.
If you would like to go back to the equation table of contents, click
on Contents.

[Algebra]
[Trigonometry]
[Geometry]
[Differential Equations]
[Calculus]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 EQUATIONS CONTAINING VARIABLES UNDER ONE OR MORE RADICALS
EQUATIONS CONTAINING VARIABLES UNDER ONE OR MORE RADICALS EQUATIONS CONTAINING VARIABLES UNDER ONE OR MORE RADICALS
EQUATIONS CONTAINING VARIABLES UNDER ONE OR MORE RADICALS
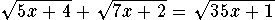
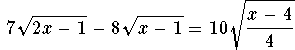
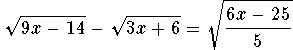
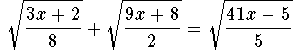

 S.O.S MATHematics home page
S.O.S MATHematics home page 