 Problems on Techniques of Integration
Problems on Techniques of Integration

Use the Integration by Parts. Set
Then
So
or
Detailed Answer.
If you prefer to jump to the next problem, click on Next Problem
below.

[Next Problem]
[Matrix Algebra]
[Trigonometry]
[Calculus]
[Geometry]
[Algebra]
[Differential Equations]
[Complex Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 Problems on Techniques of Integration
Problems on Techniques of Integration Problems on Techniques of Integration
Problems on Techniques of Integration
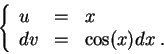
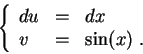

 S.O.S MATHematics home page
S.O.S MATHematics home page 