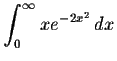
 Practice Exam: Numerical Integration, Improper Integrals, Applications
Practice Exam: Numerical Integration, Improper Integrals, Applications
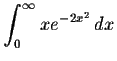
Solution: The integrand is continuous for all x, consequently the only "impropriety" occurs at ![]() .
.
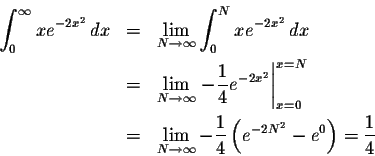
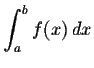 , the interval [a,b] is divided into n parts of length
, the interval [a,b] is divided into n parts of length
Solution: Let
![]() denote the endpoints of the n subintervals.
Then
denote the endpoints of the n subintervals.
Then
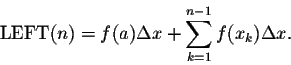
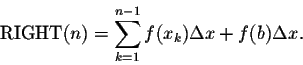
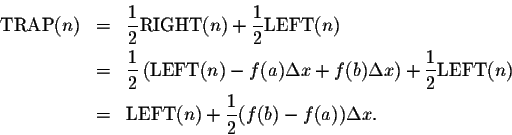

Solution: The integrand is continuous for all ![]() ,
consequently the only "impropriety" occurs at
,
consequently the only "impropriety" occurs at ![]() .
For large x-values,
.
For large x-values,
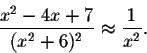
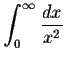 converges at infinity by the p-test, so does the integral in question.
converges at infinity by the p-test, so does the integral in question.
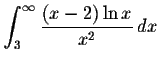
Solution: The integrand is continuous for all ![]() ,
consequently the only "impropriety" occurs at
,
consequently the only "impropriety" occurs at ![]() .
For large x-values,
.
For large x-values,
For ![]() ,
,
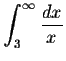 diverges.
diverges.
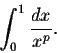
Solution: For ![]() ,
we have
,
we have
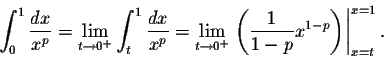
What if p=1? Then
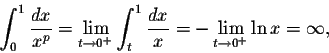
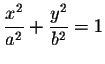 about the y-axis.
about the y-axis.
Solution: Rotating the ellipse about the y-axis amounts to rotating the graph
of
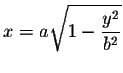 about the y-axis.
Each horizontal slice is a disk with area
about the y-axis.
Each horizontal slice is a disk with area
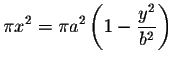 .
.
Consequently the volume of the ellipsoid is given by
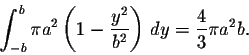

|
|
View from the Top. Darker blue corresponds to deeper water. |
Solution: The maximal distance from any point in the reservoir to the nearest shoreline is 15 km; thus the maximal depth of the reservoir is 1.5 km.
The distance to the shoreline is constant on lines parallel to the shorelines.
More precisely, the water is at least h km deep inside a rectangle of width 30-20 h km and length 50-20h km.
This leads to the Riemann sum approximation of the volume as
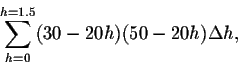
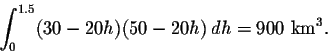
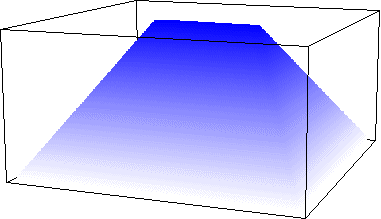
|
|
View from the Side (upside down). Darker blue corresponds to deeper water. |
